PEP 603 – Adding a frozenmap type to collections
- PEP
- 603
- Title
- Adding a frozenmap type to collections
- Author
- Yury Selivanov <yury at edgedb.com>
- Status
- Draft
- Type
- Standards Track
- Created
- 12-Sep-2019
- Python-Version
- 3.9
- Post-History
- 12-Sep-2019
Abstract
A persistent data structure is defined as a data structure that preserves the previous version of the data when the data is modified. Such data structures are effectively immutable, as operations on them do not update the structure in-place, but instead always yield a new updated structure (see [0] for more details.)
This PEP proposes to add a new fully persistent and immutable mapping
type called frozenmap to the collections module.
The bulk of frozenmap’s reference implementation is already
used in CPython to implement the contextvars module.
Rationale
Python has two immutable collection types: tuple and
frozenset. These types can be used to represent immutable lists
and sets. However, a way to represent immutable mappings does not yet
exist, and this PEP proposes a frozenmap to implement an
immutable mapping.
The proposed frozenmap type:
- implements the
collections.abc.Mappingprotocol, - supports pickling, and
- provides an API for efficient creation of “modified” versions.
The following use cases illustrate why an immutable mapping is desirable:
- Immutable mappings are hashable which allows their use
as dictionary keys or set elements.
This hashable property permits functions decorated with
@functools.lru_cache()to accept immutable mappings as arguments. Unlike an immutable mapping, passing a plaindictto such a function results in error. - Immutable mappings can hold complex state. Since immutable mappings can be copied by reference, transactional mutation of state can be efficiently implemented.
- Immutable mappings can be used to safely share dictionaries across thread and asynchronous task boundaries. The immutability makes it easier to reason about threads and asynchronous tasks.
Lastly, CPython [1] already contains the main portion of the C code
required for the frozenmap implementation. The C code already
exists to implement the contextvars module (see PEP 567 for
more details.) Exposing this C code via a public collection type
drastically increases the number of users of the code. This leads to
increased code quality by discovering bugs and improving performance
which without a frozenmap collection would be very challenging
because most programs use the contextvars module indirectly.
Specification
A new public immutable type frozenmap is added to the
collections module.
Construction
frozenmap implements a dict-like construction API:
frozenmap()creates a new empty immutable mapping;frozenmap(**kwargs)creates a mapping from**kwargs, e.g.frozenmap(x=10, y=0, z=-1)frozenmap(collection)creates a mapping from the passedcollectionobject. The passedcollectionobject can be:- a
dict, - another
frozenmap, - an object with an
items()method that is expected to return a series of key/value tuples, or - an iterable of key/value tuples.
- a
Data Access
frozenmap implements the collection.abc.Mapping protocol.
Therefore, getters, membership checks, and iteration work the same
way that they would for a dict:
m = frozenmap(foo='bar')
assert m['foo'] == 'bar'
assert m.get('foo') == 'bar'
assert 'foo' in m
assert 'baz' not in m
assert m.get('baz', 'missing') == 'missing'
assert m == m
assert m != frozenmap() # m is not equal to an empty frozenmap
assert len(m) == 1
# etc.
Mutation
frozenmap instances are immutable. That said, it is possible
to efficiently produce mutated copies of the immutable instance.
The complexity of mutation operations is O(log N) and the resulting
frozenmap copies often consume very little additional memory due
to the use of structural sharing (read [6] for more details.)
frozenmap.including(key, value)
The method creates a new frozenmap copy with a new key / value
pair:
m = frozenmap(foo=1)
m2 = m.including('bar', 100)
print(m) # will print frozenmap({'foo': 1})
print(m2) # will print frozenmap({'foo': 1, 'bar': 100})
frozenmap.excluding(key)
The method produces a copy of the frozenmap which does not
include a deleted key:
m = frozenmap(foo=1, bar=100)
m2 = m.excluding('foo')
print(m) # will print frozenmap({'foo': 1, 'bar': 100})
print(m2) # will print frozenmap({'bar': 1})
m3 = m.excluding('spam') # will throw a KeyError('spam')
frozenmap.union(mapping=None, **kw)
The method produces a copy of the frozenmap and adds or modifies
multiple key/values for the created copy. The signature of
the method matches the signature of the frozenmap constructor:
m = frozenmap(foo=1)
m2 = m.union({'spam': 'ham'})
print(m2) # will print frozenmap({'foo': 1, 'spam': 'ham'})
m3 = m.union(foo=100, y=2)
print(m3) # will print frozenmap({'foo': 100, 'y': 2})
print(m) # will print frozenmap({'foo': 1})
Calling the union() method to add/replace N keys is more efficient
than calling the including() method N times.
frozenmap.mutating()
The method allows efficient copying of a frozenmap instance with
multiple modifications applied. This method is especially useful
when the frozenmap in question contains thousands of key/value pairs
and there’s a need to update many of them in a performance-critical
section of the code.
The frozenmap.mutating() method returns a mutable dict-like
copy of the frozenmap object: an instance of
collections.FrozenMapCopy.
The FrozenMapCopy objects:
- are copy-on-write views of the data of
frozenmapinstances they were created from; - are mutable, although any mutations on them do not affect the
frozenmapinstances they were created from; - can be passed to the
frozenmapconstructor; creating a frozenmap from aFrozenMapCopyobject is an O(1) operation; - have O(log N) complexity for get/set operations; creating them is an O(1) operation;
- have a
FrozenMapCopy.close()method that prevents any further access/mutation of the data; - can be used as a context manager.
The below example illustrates how mutating() can be used with
a context manager:
numbers = frozenmap((i, i ** 2) for i in range(1_000_000))
with numbers.mutating() as copy:
for i in numbers:
if not (numbers[i] % 997):
del copy[i]
numbers_without_997_multiples = frozenmap(copy)
# at this point, *numbers* still has 1_000_000 key/values, and
# *numbers_without_997_multiples* is a copy of *numbers* without
# values that are multiples of 997.
for i in numbers:
if not (numbers[i] % 593):
del copy[i]
numbers_without_593_multiples = frozenmap(copy)
print(copy[10]) # will print 100.
print(copy[10]) # This will throw a ValueError as *copy*
# has been closed when the "with" block
# was executed.
Iteration
As frozenmap implements the standard collections.abc.Mapping
protocol, so all expected methods of iteration are supported:
assert list(m) == ['foo']
assert list(m.items()) == [('foo', 'bar')]
assert list(m.keys()) == ['foo']
assert list(m.values()) == ['bar']
Iteration in frozenmap, unlike in dict, does not preserve the
insertion order.
Hashing
frozenmap instances can be hashable just like tuple objects:
hash(frozenmap(foo='bar')) # works
hash(frozenmap(foo=[])) # will throw an error
Typing
It is possible to use the standard typing notation for frozenmaps:
m: frozenmap[str, int] = frozenmap()
Implementation
The proposed frozenmap immutable type uses a Hash Array Mapped
Trie (HAMT) data structure. Functional programming languages,
like Clojure, use HAMT to efficiently implement immutable hash tables,
vectors, and sets.
HAMT
The key design contract of HAMT is the guarantee of a predictable value when given the hash of a key. For a pair of key and value, the hash of the key can be used to determine the location of value in the hash map tree.
Immutable mappings implemented with HAMT have O(log N) performance
for set() and get() operations. This efficiency is possible
because mutation operations only affect one branch of the tree,
making it possible to reuse non-mutated branches, and, therefore,
avoiding copying of unmodified data.
Read more about HAMT in [5]. The CPython implementation [1] has a fairly detailed description of the algorithm as well.
Performance
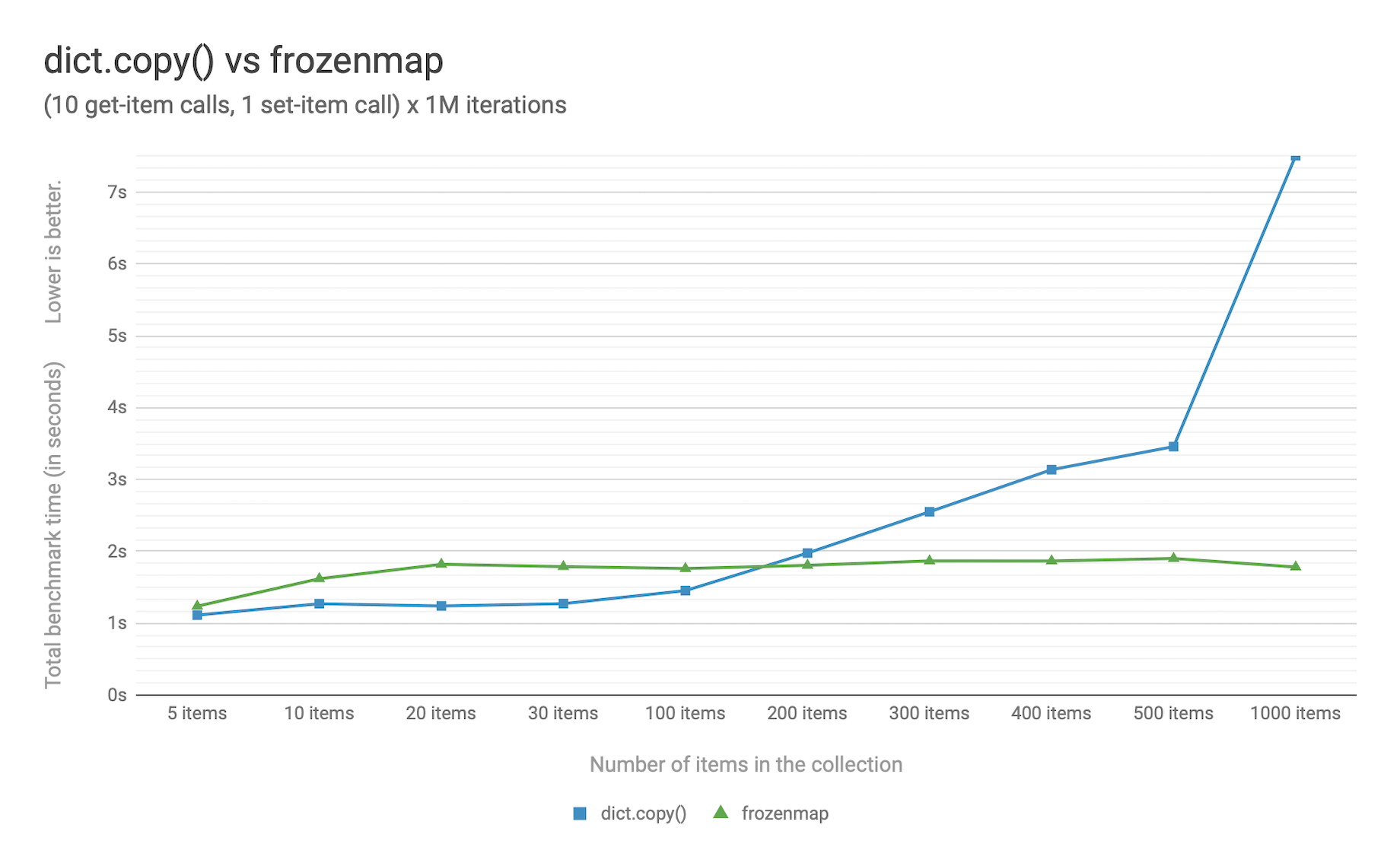
Figure 1. Benchmark code can be found here: [3].
The above chart demonstrates that:
frozenmapimplemented with HAMT displays near O(1) performance for all benchmarked dictionary sizes.dict.copy()becomes less efficient when using around 100-200 items.
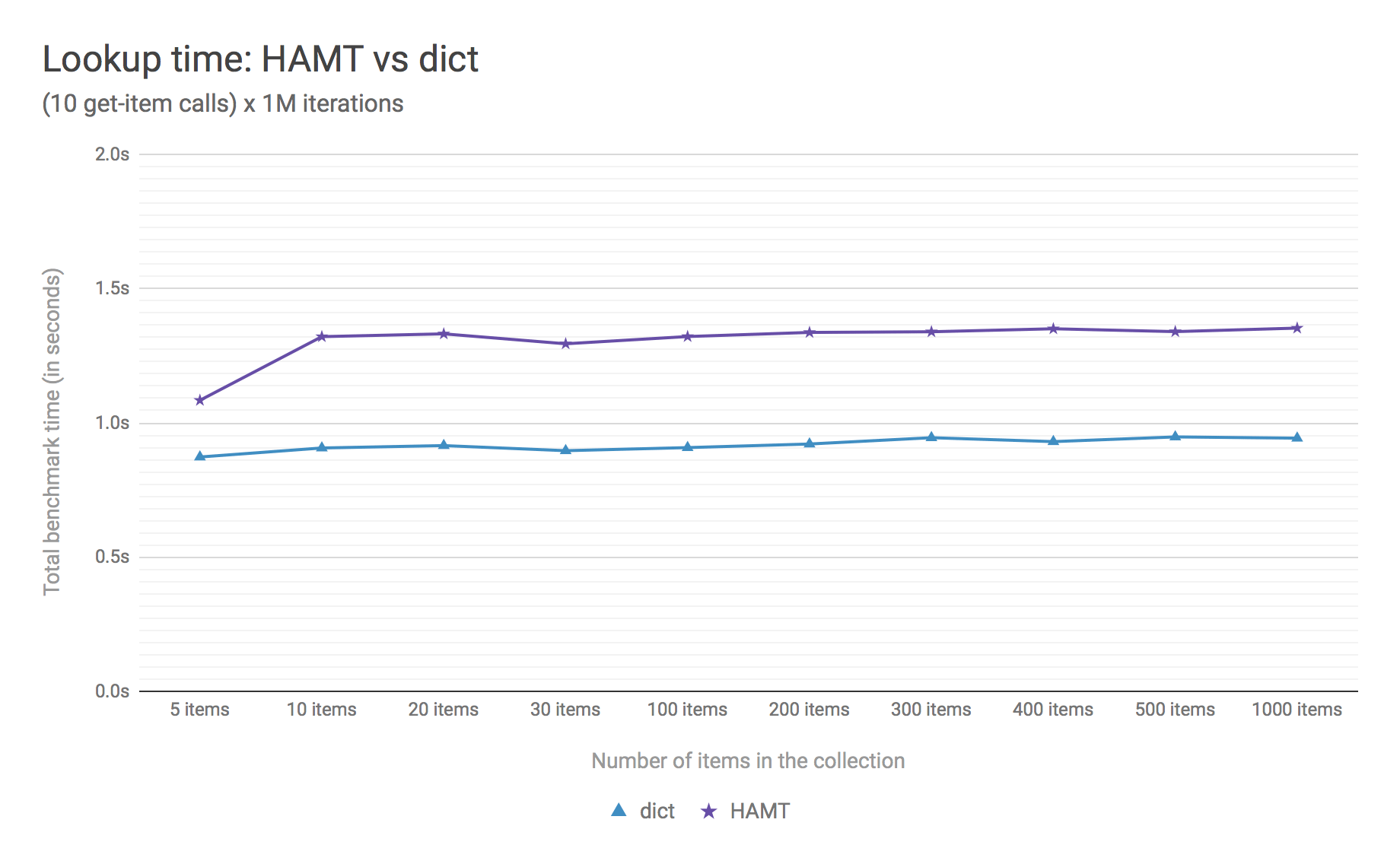
Figure 2. Benchmark code can be found here: [4].
Figure 2 compares the lookup costs of dict versus a HAMT-based
immutable mapping. HAMT lookup time is ~30% slower than Python dict
lookups on average. This performance difference exists since traversing
a shallow tree is less efficient than lookup in a flat continuous array.
Further to that, quoting [6]: “[using HAMT] means that in practice while insertions, deletions, and lookups into a persistent hash array mapped trie have a computational complexity of O(log n), for most applications they are effectively constant time, as it would require an extremely large number of entries to make any operation take more than a dozen steps.”
Design Considerations
Why “frozenmap” and not “FrozenMap”
The lower-case “frozenmap” resonates well with the frozenset
built-in as well as with types like collections.defaultdict.
Why “frozenmap” and not “frozendict”
“Dict” has a very specific meaning in Python:
- a dict is a concrete implementation of
abc.MutableMappingwith O(1) get and set operations (frozenmaphas O(log N) complexity); - Python dicts preserve insertion order.
The proposed frozenmap does not have these mentioned
properties. Instead, frozenmap has an O(log N) cost of set/get
operations, and it only implements the abc.Mapping protocol.
Implementation
The full implementation of the proposed frozenmap type is
available at [2]. The package includes C and pure Python
implementations of the type.
See also the HAMT collection implementation as part of the CPython project tree here: [1].
References
- [0]
- https://en.wikipedia.org/wiki/Persistent_data_structure
- [1] (1, 2, 3)
- https://github.com/python/cpython/blob/3.8/Python/hamt.c
- [2]
- https://github.com/MagicStack/immutables
- [3]
- https://gist.github.com/1st1/be5a1c10aceb0775d0406e879cf87344
- [4]
- https://gist.github.com/1st1/dbe27f2e14c30cce6f0b5fddfc8c437e
- [5]
- https://en.wikipedia.org/wiki/Hash_array_mapped_trie#cite_note-bagwell-1
- [6] (1, 2)
- https://en.wikipedia.org/wiki/Persistent_data_structure#Trees
Acknowledgments
I thank Carol Willing, Łukasz Langa, Larry Hastings, and Guido van Rossum for their feedback, ideas, edits, and discussions around this PEP.
Copyright
This document is placed in the public domain or under the CC0-1.0-Universal license, whichever is more permissive.
Source: https://github.com/python-discord/peps/blob/main/pep-0603.rst
Last modified: 2022-03-11 20:41:57 GMT